Multiple Comparisons - Make your boss happy with false positives

name: inverse
class: center, middle, inverse

# Multiple Comparisons
## Make your boss happy with false positives - Guaranteed!
[Chris Stucchio](https://www.chrisstucchio.com) - [VWO](https://vwo.com)

---
class: center, middle
# Conversion rate optimization

[CRO](https://en.wikipedia.org/wiki/Conversion_rate_optimization) is the practice of optimizing a website to increase the number of people *converting* (making a purchase, signing up, providing an email address).

---
## Multiple creative choices

![advertise on patch](patch_advertise_green.png)

---
## Multiple creative choices

![advertise on patch](patch_advertise_purple.png)

---
## Multiple creative choices

![advertise on patch](patch_advertise_pink.png)

---
class: center, middle
# Goal
## Find the one with the highest *conversion rate*

CR(version) = P( visitor buys advertising | version )

(Hint: purple was the winner.)

---
class: center, middle
# Trading

## Predict future price of a security or portfolio.
## Buy when price is expected to go up in future
## Sell when future arrives.

---
## Trading

Between Aug 18 and Aug 24, the S&P 500 lost approximately 10% of it's value.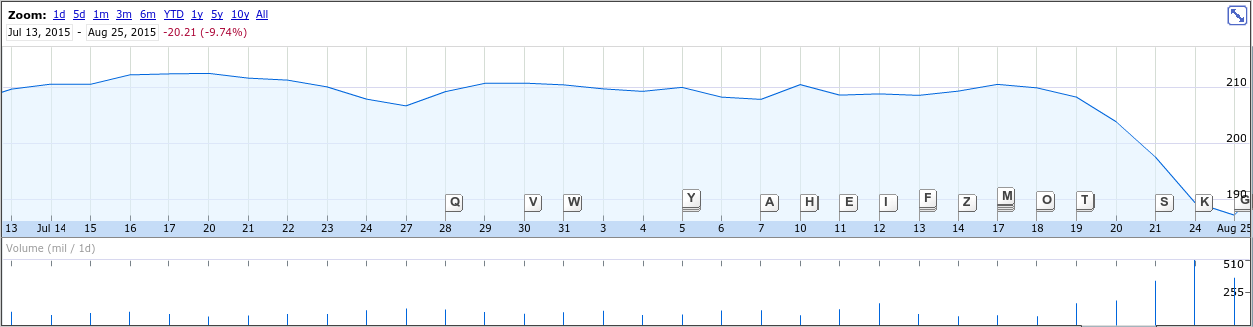

![SPY crashing](spy_predict_future_1.png)

My prediction: everyone's getting crazy afraid because of China, but this won't last.

## Aug 25: I predicted SPY will go back up...

## ...and I put about $38,000 where my mouth is.
---
## Trading

What happened?

![SPY crashing](spy_predict_future_2.png)

## Sep 17: My SPY shares are now worth $40,000.

## Am I smart, or was this just a fluke?

---
class: center, middle
# Goal
## Find a strategy with long term growth, minimal risk

$$ \textrm{maximize} ~ \frac{E[r_p - r]}{E[\sigma]} $$

$@ r_p $@ is growth rate of my portfolio, $@ r $@ is risk-free rate of return, $@ \sigma $@ is standard deviation of my portfolio's excess return.

(This is called the **Sharpe Ratio**, and is a simple example of trading objective function.)

---
class: center, middle
# Evaluating a Strategy

---
# Evaluating a Strategy
## Conversion rate Optimization

Run an A/B test.

- 50% of users see **Control**
- 50% of users see **Variation**

---
# Evaluating a Strategy
## Conversion rate Optimization
Measure conversion rate of each variation, let $@ t = c_v/n_v - c_c/n_c $@ be a *test statistic*.

Define:

$$ p = P(t > t_{exp} ~|~ \textrm{null hypothesis}, n_v, n_c ) $$

Probability of seeing results at least as "extreme" as experimental results in a hypothetical A/A test.

If $@ p < 0.05 $@, choose **Variation** otherwise choose **Control**.

Will incorrectly choose **Variation** 5% of the time when **Variation** and **Control** are identical.

---
# Evaluating a Strategy
## Trading

Run a **backtest**.

**Train** the model on historical data, say Jan 2014-Sep 2015.

**Run** the strategy on historical data, say Sep 2015-Oct 2015.

**Measure** the profit/loss in the testing period, and compute a Sharpe Ratio.

If the Sharpe Ratio is sufficiently high, deploy the strategy.
---
class: center, middle
# tl;dr; How Single Comparisons Work

---
# Multiple Comparisons

Multiple comparisons are when you do single comparisons repeatedly.

---
# Repeated peeks

Run an A/B test, but "peek" at the results every day.

- Mon: 5% chance of a false positive
--

- Tues: 5% chance of a false positive today, 9.75% false positive chance cumulatively
--

- Wed: 5% chance of a false positive, 14.3% false positive chance cumulatively

If you repeatedly peek at a test, your odds of a false positive grow to near certainty.

(This problem is resolved with VWO and Optimizely.)

---
# Segmentation

- [Segment or Die](http://online-behavior.com/targeting/segment-or-die-214) and [Segment Absolutely Everything](http://www.kaushik.net/avinash/excellent-analytics-tip2-segment-absolutely-everything/)
- [How to Analyze Your A/B Test Results with Google Analytics](http://conversionxl.com/analyze-ab-test-results-google-analytics/)

Basic idea. An A/B test was run, and returned a null result.

## No difference between test variations.

...Look at the test results at least across these segments...Desktop vs Tablet/Mobile...New vs Returning..."

---
# Segmentation

Experimental data. Ran an A/B we ran with 10,023 visitors for variation A and 10,097 for B. No difference, p=0.16. Both variations had approximately a 5% conversion rate.

Went to google analytics and broke into segments.

- Mobile/Tablet - insignificant result (p=0.35)
- East coast - insignificant (p=0.25)
- West Coast - insignificant (p=0.47)
- Organic - **significant** (p=0.043) (B is the winner)
- PPC - insignificant (p=0.16)
- Apple users - insignificant (p=0.31)
- Socially referred traffic - insignificant (p=0.76)

Set up targeting, hit organic traffic with version B, everyone else with A. **Win!**

---
class: center, middle
# I lied

---
# Segmentation

Data is simulated.

**Both A and B have identical 5% conversion rates.**

a_conversions = bernoulli(0.05).rvs(10023)
    b_conversions = bernoulli(0.05).rvs(10097)

- "Mobile/Tablet" is the first 5,000 samples (`a_conversions[0:5000]`) and "Desktop" is the remainder (`a_conversions[5000:]`).
- "East coast" is the 1st, 2nd, 4th, 5th, 7th, 8th, etc visitor. "West coast" is the 3rd, 6th, 9th, etc.
- Other segments are similarly **made up**.

So how come our A/B test said variation B wins for organic traffic?

---
class: center, middle
## Probability of false positive
## 1 segment

## $$1-(1-0.05)^1 = 0.05$$
---
class: center, middle
## Probability of false positive
## 2 segments

## $$ 1-(1-0.05)^2 = 0.0975 $$
---
class: center, middle
## Probability of false positive
## 5 segments

## $$ 1-(1-0.05)^5 = 0.226 $$
---
class: center, middle
## Probability of false positive
## 15 segments

## $$ 1-(1-0.05)^{15} = 0.537 $$
---
# Segmentation for fun and profit
- Step 1: Run an A/B test.
- Step 2: Segment or Die.
- Step 3: Find a false positive and show your boss.
- Step 4: Get promoted

Repeat as needed.
---
# Multiple goals

Most A/B testing tools give you the ability to track multiple goals:

- **Primary Goal**: Revenue
- **Goal 2**: Mailing list signups
- **Goal 3**: Add to cart
- **Goal 4**: Reads at least 3 pieces of content
- **Goal 5**: Visitor returns

## "Even if the variation doesn't make revenue go up, more email signups are good, right?"

---
class: center, middle
## Probability of false positive
## 1 goal

## $$1-(1-0.05)^1 = 0.05$$
---
class: center, middle
## Probability of false positive
## 2 goals

## $$ 1-(1-0.05)^2 = 0.0975 $$
---
class: center, middle
## Probability of false positive
## 5 goals

## $$ 1-(1-0.05)^5 = 0.226 $$
---
# Fishing for strategies

Consider an idea for a strategy - say, pairs trading.

Take two "similar" securities, e.g. GOOG and FB.
![GOOG_FB](goog_fb_pair.png)

---
# Fishing for strategies

![GOOG_FB](goog_fb_pair.png)

On Sep 24:

- Buy 10 shares of GOOG @ $591.59 - cost $5915.90.
- Sell 62 shares of FB short @ $94.41 - gain $5853.42.

---
# Fishing for strategies

![GOOG_FB](goog_fb_pair.png)

On Oct 2:

- Sell 10 shares of GOOG @ 642.36 - gain $6423.60
- Buy 62 shares of FB @ $94.41 and close short - cost $5708.34

---
# Fishing for strategies

Net:

- $-5915.90 (buy GOOG)
- $5853 (sell FB short)
- $6423.60 (sell GOOG)
- $-5708.34 (buy FB, close short)

-----------
Gain: $652.78

---
# Fishing for strategies

Semi-arbitrary choices to be made:

- Tried GOOG/TWTR, didn't work. Had to play around until I found GOOG/FB which worked.
- Trade duration - I was looking for 5-15 day trades, why not 15-30 day trades?
- Trade amplitude - how far apart should the two lines be before I open a trade?

---
# Fishing for strategies

General process for developing a strategy.

1. Come up with strategy idea, with free parameters (trade duration, specific pairs, amplitude).
2. Train based on historical data - say 0-Aug 2015.
3. Backtest - did we turn a simulated profit in Sep 2015-Oct 2015? If not, GOTO 1.
4. Deploy it and get rich!

---
class: center, middle

# **$8,747**

## How much I lost on pairs trading
---
# Fishing for strategies

## Probability of the backtest giving me a bad result the first time:

## $$ 1-(1-0.05)^1 = 0.05 $$

(Stylized fact)

---
# Fishing for strategies

## Probability of the backtest giving me a bad result once in 2 strategies

## $$ 1-(1-0.05)^2 = 0.0975 $$

(Stylized fact)

---
# Fishing for strategies

## Probability of the backtest giving me a bad result at least once in 15 strategies

## $$ 1-(1-0.05)^{15} = 0.537 $$

(Stylized fact)

---
class: center, middle

# The problem

---
# Multiple Comparisons

Core problem. N comparisons:

$$
P(\textrm{find false winner} ~|~ \textrm{Null Hypothesis}) = 1 - (1-0.05)^N
$$

$$
\approx 0.05 \cdot N
$$

---
# Re-use of training data
## A sneaky way to cheat

If I ever GOTO 1, then I just used *test* data to develop my *strategy*. That's cheating!

## Multiple comparisons on steroids!

---
# Re-use of training data

![overfit](data_to_overfit.png)

$@ y_i = x_i + g $@, $@ g $@ being gaussian noise

---
# Re-use of training data

![overfit](data_to_overfit_w_fit.png)

Plotted with a 10th order polynomial fit - fits training data perfectly!

---
# Re-use of training data

![overfit](data_to_overfit_w_fit_new_pts.png)

Not such an accurate prediction. Lets go back to step 1, new model!

---
# Re-use of training data

![overfit](data_to_overfit_w_fit_new_pts_data_reuse.png)

I used training data and found a better model!

**Fits test data**

---
# Re-use of training data

![overfit](data_to_overfit_w_fit_new_pts_data_reuse_oops.png)

---
# Reuse of training data

1. Peek at data.

2. Choose a test statistic, and compute p-value:

$$
p = P(\textrm{find false winner} ~|~ \textrm{Null Hypothesis})
$$

3. Right thing to compute (but very hard):

$$
p^\star = P(\textrm{find false winner} ~|~ \textrm{Null Hypothesis}, \textbf{peek})
$$

Andrew Gelman calls this [The Garden of Forking Paths](http://www.stat.columbia.edu/~gelman/research/unpublished/p_hacking.pdf).

---
class: center, middle, inverse
# How to fix it

---
# Sidak Correction

Can fix this with adjusted p-values. If the p-value cutoff for the *ensemble* of tests is $@ p $@, then for any *individual* test the cutoff is:

$$
p^\star = 1 - (1-p)^{1/N}
$$

Works because:

$$
1-(1-p^\star)^N = 1-(1-[1 - (1-p)^{1/N}])^N
$$
$$ = 1-([1-p]^{1/N})^N = p $$
---
# Sidak Correction

Example:

- 16 segments
- p-value cutoff of 5%.

$$
p^\star = 1 - (1-0.05)^{1/16} = 0.0032
$$

So if any *individual* segment has a p-value below 0.32%, then test found a significant result with p-value below 5%.

---
# Sidak Correction

- Segment 1: p-value 0.15
- Segment 2: p-value 0.30
- Segment 3: p-value 0.01
- Segment 4: p-value 0.75
- ...

**No significant results**

---
# Sidak Correction

**Problem:** Consider a test with 5% base conversion rate and attempting to measure a 10% lift with an 80% probability (p-value cutoff of 5%).

- 1 segment: 30,244 samples per variation
- 2 segments: 36,433 samples per variation
- 6 segments: 46,344 samples per variation
- 16 segments: 55,131 samples per variation.

So to run the A/B test you need 60,000 visitors.

If you want to segment you need 882,000 visitors!

---
class: center, middle
# Hierarchical Models

---
# Hierarchical Models

Hierarchical models work great for CRO.

**Global effect** $@ \alpha $@ - the effect of the *variation*.

**Segment effect** $@ \beta_i $@ - the effect of the *segment*.

**Individual conversion rate** - $@ \lambda_i = \alpha + \beta_i $@ "in spirit"

$@ \lambda_1 $@ and $@ \lambda_2 $@ are coupled through global effect.

Better use of data *if model is valid*, since data on segment 1 contributes *some* information about segment 2.

**Prior choice very important here**

---
# Hierarchical Models

![hierarchical modelling](hierarchical_model.png)

---
# Differential privacy

Aggregate function is *differentially private* if it doesn't leak information about *individuals*.

**NOT differentially private:** Sum.

- Let x = Sum(salary_at_VWO)
- Chris Quits!
- Let y = Sum(salary_at_VWO)

Chris salary = x-y.

---
# Differential privacy

Things which are differentially private:

- Adding Laplacian noise: $@ f(x) + z $@
- [Bootstrap Aggregation](https://en.wikipedia.org/wiki/Bootstrap_aggregating) - a fairly common statistical operation.
- [Bayesian Posterior Sampling](http://arxiv.org/pdf/1306.1066v4.pdf) - compute a posterior, draw a sample of limited size and compute all queries on the sample.

---
# Differential privacy

![overfit](data_to_overfit_w_fit_new_pts_data_reuse.png)

## Overfitting is memorization.

---
# Differential privacy

![overfit](data_to_overfit_w_fit_new_pts_data_reuse.png)

## Can't overfit what you don't know

---
# Conclusion

Multiple comparison problems are everywhere.

Most data analysis is a garden of forking paths.

Data reuse is everywhere.

[Google analytics reports no change when you deploy your big winners](http://blog.sumall.com/journal/optimizely-got-me-fired.html)

[Results don't replicate](https://en.wikipedia.org/wiki/Replication_crisis)

[Traders lose millions due to overfitting](http://www.ams.org/notices/201405/rnoti-p458.pdf)

The world is ending.

---
# References

[The Garden of Forking Paths](http://www.stat.columbia.edu/~gelman/research/unpublished/p_hacking.pdf) by Andrew Gelman.

[The Reusable Holdout: Preserving Statistical Validity in Adaptive Data Analysis](http://rsrg.cms.caltech.edu/netecon/privacy2015/slides/hardt.pdf)

[Gelman's Hierarchical Modelling Book](http://www.amazon.com/gp/product/052168689X/ref=as_li_tl?ie=UTF8&camp=1789&creative=390957&creativeASIN=052168689X&linkCode=as2&tag=christuc-20&linkId=EYSTJKJSMEZAV6TK)

[Pseudo-Mathematics and Financial Charlatanism: The Effects of Backtest Overfitting on Out-of-Sample Performance](http://www.ams.org/notices/201405/rnoti-p458.pdf)

[The probability of Backtest Overfitting](http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2326253)