All About Conversion Rates

name: inverse
class: center, middle, inverse

# Conversion Rates
## And how to measure them
### From a bayesian point of view
Chris Stucchio, [BayesianWitch](http://www.bayesianwitch.com)

---
name: inverse
class: center, middle, inverse
# Conversion Rate

Conversion rate is the probability of a **visitor** converting to a **customer**.

Click here to learn ONE WEIRD TRICK
    for becoming taller!

http://www.growtaller.com

[Details on this can be found on my blog](http://www.chrisstucchio.com/blog/2013/bayesian_analysis_conversion_rates.html)
---

# Conversion Rate

"True" conversion rate:

ctr = P( conversion | visitor )

Empirical conversion rate:

# of conversions / # of visitors

## Not the same thing

Relation between empirical and true conversion rate:

P( # conversions = C | # visitors) = Const * ctr^(C)(1-ctr)^(# visitors - C)

---

# Example: A coin

"True" conversion rate:

ctr = P( conversion | visitor ) = 0.5

Empirical conversion rate:

6 heads / 10 clicks = 0.6

## Not the same thing

Approximately, but not identically equal.

---

# True conversion rate

Can never be known exactly. But we can estimate it based on:

## Prior Knowledge

A 90% conversion rate is crazy because 30% of people are already tall enough. The most we'll ever get is 70%.

## Data

I showed the ad to 1024 people and 37 clicked it. Pretty sure the conversion rate is far less than 70%.

---
# Probability distributions

In code:

In [20]: ctr
    Out[20]:
    array([ 0.  ,  0.01,  0.02,  0.03,  0.04,  0.05,  0.06,  0.07,  0.08,
            0.09,  0.1 ,  0.11,  0.12,  0.13,  0.14,  0.15,  0.16,  0.17,
            ...
            0.81,  0.82,  0.83,  0.84,  0.85,  0.86,  0.87,  0.88,  0.89,
            0.9 ,  0.91,  0.92,  0.93,  0.94,  0.95,  0.96,  0.97,  0.98,  0.99])

In [33]: pctr
    Out[33]:
    array([  1.81296534e-01,   1.49781508e-01,   1.23505113e-01,
             1.01637144e-01,   8.34724053e-02,   6.84129001e-02,
             ...
             4.98344117e-28,   2.10713975e-30,   9.50515970e-34,
             1.81296534e-39])

Important fact:

In [29]: pctr.sum()
    Out[29]: 1.0000000000000004

---
# Probability distributions

## Interpretation

`pctr[0]` represents the probability that the true conversion rate is 0%.

`pctr[1]` represents the probability that the true conversion rate is 1%.

etc.

---
# Probability distributions

## What is probability that CTR is between 10% and 30%?

In [35]: pctr[where(logical_and(ctr >= 0.1, ctr =< 0.3))].sum()
    Out[35]: 0.12225830312891443

---

# Probability distributions

![test](example_pdf_1.png)

ctr is unknown, could be anything

---
# Probability distributions

![test](example_pdf_2.png)

ctr is approximately 20%, could be between 5% and 45%.

---
# Probability distributions

![test](example_pdf_3.png)

ctr is between 50% and 70%.

---
class: center, middle

![your opinon](your_opinion.png)

---
# In my uneducated opinion

## Stating your prior

![prior](prior.png)

What it means: I think a low CTR is far more likely than a high one.

---
class: center, middle
# "...when events change, I change my mind. What do you do?"
## Paul Samuelson

(Often incorrectly attributed to Keynes.)

---
# Changing your opinion

In Bayesian Statistics, one's opinion changes based on Bayes Rule.

P(evidence|ctr) P(ctr)
    P(ctr|evidence) = ----------------------
                           P(evidence)

Given an old opinion `P(ctr)`, you have a clear rule for changing your opinion.

---
# Changing your opinion

Evidence: Showed the advertisement to a user and they clicked

P(evidence|ctr) = ctr

Doing some math:

ctr * P(ctr)
    P(ctr|evidence) = ------------
                       P(evidence)

In code:

def update_belief_from_click(pctr):
        unnormalized = ctr * pctr
        return unnormalized / unnormalized.sum()

---
# Changing your opinion

What we believe before evidence:

![prior](prior.png)

---
# Changing your opinion

What we believe after seeing evidence:

![prior](posterior_one_click.png)

---
# Changing your opinion

Evidence: Showed the advertisement to a user and they did NOT click

P(evidence|ctr) = 1 - ctr

Doing some math:

(1 - ctr) * P(ctr)
    P(ctr|evidence) = ------------
                       P(evidence)

In code:

def update_belief_from_no_click(pctr):
        unnormalized = ctr * pctr
        return unnormalized / unnormalized.sum()

---
# Changing your opinion

What we believe after seeing one click:

![prior](posterior_one_click.png)

---
# Changing your opinion

What we believe after seeing one click, but 4 displays with no clicks:

![prior](posterior_one_click_4_noclick.png)

---
# Changing your opinion

What we believe after seeing one click, but 20 displays with no clicks:

![prior](posterior_one_click_20_noclick.png)

---
# Changing your opinion

What we believe after seeing 4 clicks and 203 displays with no clicks:

![prior](posterior_lots_of_displays.png)

---
# Disagreement

My opinion and BG's might differ:

![prior](two_opinions_prior.png)

---
# Disagreement

After we gather enough data, they will converge:

![prior](two_opinions_posterior.png)

---
class: center, middle
# Opinions and Actions

[More details on the BayesianWitch blog](http://www.bayesianwitch.com/blog/2014/bayesian_ab_test.html)
---
# A decision to make

## Designer's Choice

![advertise on patch](patch_advertise_green.png)

---
# A decision to make

## Sales Guy Choice

![advertise on patch](patch_advertise_red.png)

---
# A decision to make

## Analytical Marketer: "Don't forget to try pink and purple"

![advertise on patch](patch_advertise_purple.png)

---
# A decision to make

## Analytical Marketer: "Don't forget to try pink and purple"

![advertise on patch](patch_advertise_pink.png)

---
# How do we choose?

## Difficulties

- Non-zero probability of making mistake
- Must stop test, if only to delete code
- How long must we run it for?
- Can we stop the test early?

---
# Important parameters

## Prior

Already talked about this.

## Threshold of caring

Suppose version A converts at 20% and version B converts at 10%. You definitely care.

Suppose A converts at 10% and B converts at 10.01%. You probably don't care.

threshold_of_caring = Above this I care, below this I don't.

---
# A/B testing

Some data:

<table>
<tr><th>Version</th><th>Displays</th><th>Conversions</th></tr>
<tr><td>A</td><td>581</td><td>112</td></tr>
<tr><td>B</td><td>583</td><td>75</td></tr>
</table>

Now what do we do? Stop the test and choose B? Continue the test?

## What if we made a mistake?

---
# Joint Probability Distribution

Ran test for A and B individually. Computed posteriors.

![ab test posteriors](ab_test_posteriors.png)

---
# Joint Probability Distribution

![ab test posteriors](ab_test_joint_probability_distribution.png)

Point in plane is `(ctrA, ctrB)`. Color is probability density.

---
# Consequences of an error

## Assume B > A, but we choose A

Loss = sum( (ctrA - ctrB) * P(ctrA, ctrB | ctrA > ctrB) )

Sum is taken over all values of `(ctrA, ctrB)` for which `ctrA > ctrB` (above yellow line):

---
# Stopping condition

if loss < threshold_of_caring:
        stop_test_choose(B)
    else:
        continue_test()

Stop test when the amount of lift we expect to lose **assuming** we make the wrong choice is so low that we don't care. Otherwise continue.

## Benefits

- Lets us stop tests early.
- Or run them for extra time if we need to.
- Can incorporate a more detailed model than simply 1 conversion rate, if needed.

## Drawbacks

- Standard frequentist test takes a couple of microseconds and 2 doubles.
- Bayesian test requires up to 1 second and 1024x1024 array of doubles (16mb ram).

---
## Why history chose frequentist methods

![old timey computer](old_timey.jpg)

---
class: center, middle
# Bandit Algorithms

[More details on my blog](http://www.chrisstucchio.com/blog/2013/bayesian_bandit.html)

---
# Limitations of A/B test

- While test is running users see bad version 50% of time
- Requires human thought
- Requires lots of samples

## Bandit Algorithms

---
# Find Balance

# Exploration

Time spent testing different versions to see which is best.

# Exploitation

Showing users the best version

---
# Bayesian Bandit

## Thomson Sampling

def display_choice(posteriors):
        ranking = {}
        for (variation, posterior) in posteriors:
            ranking[variation] = posterior.sample()
        return argmax(ranking)

Or, since this is a functional programming crowd:

def display_choice(posteriors):
        return argmax(
          posteriors.map(
              (variation, posterior) => (variation, posterior.sample) )
          )

---
# Most of the time

![common case](bandit_algorithm_common.png)

---
# Most of the time

![common case](bandit_algorithm_common.png)

---
# Occasionally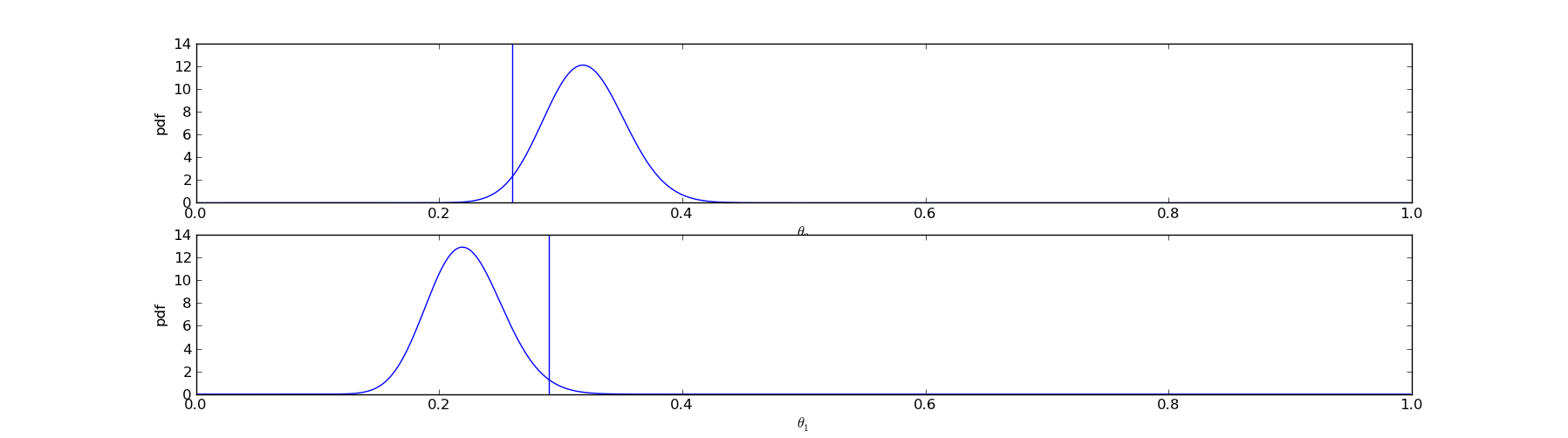

![common case](bandit_algorithm_uncommon.png)

---
# Eventually

![common case](bandit_algorithm_eventual.png)

Probability of making wrong choice by chance (oversimplified):

P(wrong choice) = O( exp( -N * delta ) )

Here `N` is the number of samples, and `delta` is the lift between the best and worst version.

---
# Asymptotics

A/B testing:

Loss = N * P(error) = O(N)

Thompson Sampling:

Loss = O(log(N))

(Logarithmic regret is the *best possible gain*.)

[Math details are here](http://arxiv.org/pdf/1111.1797.pdf)

---
# Use Cases

Bandit algorithms great for *automatic optimization*.

## Long Tail SEO marketing

10,000 SEO-optimized pages, each with low traffic:

- "Best dress to wear for Mexican wedding"
- "Best dress to wear for first date"
- "Best dress to wear for {{event}}"...

## Rapidly changing content

- "Valentines day Sale, only 3 days remaining."
- "Spring sale, this weekend only!"

- "Man Bites Dog!"
- "Headless Body found in Topless Bar"

---
# Use Cases

## 10,000 pages

Use bandit algorithm to choose which photo/description of the dress to display.

## Short term sales

Use bandit algorithm to determine best title of the sale

## News publishing

Use bandit algorithm to determine which story to promote.

---
class: center, middle, inverse
# "We #&@!ing lost $400,000 because you %@#$ing forgot the A/B test was still %@&#ing running?!?!?!"
## Source: Anonymous

---
# Quantitative results

Ran bandit algorithm to optimize content on a large number of SEO-optimized microsites.

![bandits for seo pages](bandits_for_seo_pages.png)

Outperformed both A/B testing and random selection.

---
# Conclusions

## Use A/B testing for long term feature decisions
## Use Bandit Algorithms for Transient/high volume content
## Use Bayesian Statistics